Attack of the Buddahbrot
A few months ago I purchased a fantastic book from a dusty local bookshop almost purely on the basis of it's fascinating name: The Magic Machine - A Handbook of Computer Sorcery; indeed, I have the hardback edition but I do like the somewhat retro cover of the paperback on Amazon.
In case you were too lazy to click the above link then allow me to present the description as detailed on the Amazon store page:
This is the second collection of A. K. Dewdney's popular "Computer Recreations" columns, drawn from "Scientific American". The author discusses some of today's hottest topics including chaos, computer viruses, and artificial landscapes. The computer recreations described here range from purely entertaining brain teasers to more practical computer applications of scientific thought. 26 programs are included that require only moderate programming skills. There are Mathemagical movies, a miniature universe, puzzles, wordplay, and simple programs that produce striking effects. Dewdney's clear directions allow homecomputer owners to sit at the computer and try each one of them.
"Today's hottest topics" being interesting computer based topics from around the mid to late 80s - but nevertheless I found the book enthralling, I couldn't stop reading it. I think the reason for this is that these were the hot topics when I was growing up and starting to cut my programming teeth with BASIC on the Atari ST. I vividly remember seeing the Mandelbrot set for the first time on TV and soon obtained a program on a magazine cover disk that allowed me to explore it for myself.
The first chapter of Dewdney's book describes the set and how it's generated and without hesitation I put the book down, fired up XCode and had it drawing on my screen about thirty minutes later (having faffed about SDL sorted for easy hassle free frame buffer access and keyboard input - I've still not got around to sitting down properly with Cocoa Programming for Mac OS X to learn the Apple way of doing it). I played around with the program a bit, making it cycle the colour palette giving a particularly trippy effect, and then it dawned on me to compile it as a 64-bit application so as to obtain even greater magnification. For some reason I found it particularly amusing to keep zooming until I'd maxed out the resolution of a 64-bit floating point variable, as you start to run out of bits to work with the display gets progressively blockier as you'd expect, and then you zoom back out to see just how far in you've gone.
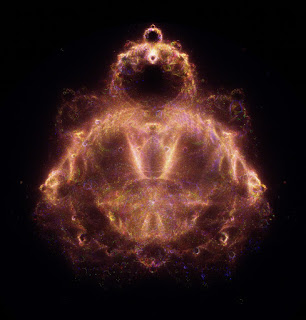
Following the recent passing of Benoît Mandelbrot I was snooping around again and suddenly stumbled across the Buddahbrot. This is a way of visualising the inner workings of the set - a recursive complex-number calculation where a series of complex numbers are tested one after the other. Essentially after n-iterations points tested will either lie within the set, or they'll have gone AWOL and made for the moon. In the traditional renderings of the set the black portions actually represent numbers which lie within the set, the coloured areas representing the points which have escaped, and the colour chosen indicates how quickly they escaped.
Dewdney's book has a section where he describes a tour on the Mandelbus, an imaginary bus on the complex plane which starts at a given point and follows the path of the calculation of that point. It is in fact this bus' route that is rendered when generating the Buddahbrot. For every point determined to lie within the set, it's calculation is repeated and for each position it visits we chalk up another hit in the output array. I played around with settings and colours, and decided that I wanted to see an even bigger view of the Buddahbrot I was rendering. Unfortunately 'zooming in' does not work as it does with the typical Mandelbrot rendering; Since the points can and do move about wildly during calculations what you see in your window will result on points outside of it, so the only real way to get in closed is to render a larger image. Last night I generated two 4800x3200 pixel images (dumped out as raw image data at the end of the render process) which I then imported into GIMP to scale and save for the web - the raw data being standard 32-bit ARGB data clocked in at just shy of 60 megabytes. Despite scaling my output data so that contrast was stretched fully across the available range in an attempt to get good output, I didn't reckon on such a skewed distribution of values. The vast majority (99% at a guess) of pixels ended up with colour values in the 0-16 range, so a few curve tweaks really brought out the best of the detail albeit with the associated detail loss. You can see the (cropped and scaled) result below. Moving forward I'll modify the contrast stretch to use a histogram equalisation as in simply scaling by the maximum values I clearly lost a huge amount of colour resolution for most of the image.
JPEG of the first rendered image, click for big! Even in this scaled down image you can see some of the intricate detail.
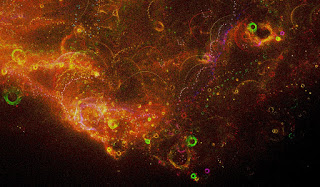
I pretty much a large part of the day in awe of various renderings, 1200x800 pixel images were quite quick to create, and watching them draw was also interesting; I currently have a black/purple ankle which I can't walk on so the day was well spent exercising my imagination/brain instead of my body. The large render took a little over 90 minutes to complete, using 131,072 (yes, I like powers of two) iterations for the red channel, 262,144 for the green and twice as many again for the blue channel. I modified the colour curves in GIMP but it was these different iteration values which account for the distinct different-coloured features. Also I used rand() to determine which points to iterate (varying the probability of rejection for each colour channel) and this is what causes the non-symmetrical nature of the image. Next up I intend to make an even larger render to see more detail, but that will have to wait until I can sit at a table - maxing out the CPU for an hour and a half was bad enough with the machine on my lap while I did other things!
JPEG of part of the second render at 100%, hopefully modifying my colour scaling will result in a less 'noisy' image, but that's only a guess on my part at the moment - I'm pretty sure it'll also require an increased number of iterations.